当我们优化损失函数时，我们在优化什么

更新时间：2024-07-22 07:46:15

高能预警：本文涉及大量的数学推导，如有不适，概不负责。

在回归问题（regression problems）中，我们常用平方误差和（sum of squares）来衡量模型的好坏。

回归问题可以定义如下：

给定一个包含 $N$ 个数据的训练集 $\\mathbb x\\equiv\\{x_1,x_2,\\dots,x_N\\}$ ，以及这些数据对应的目标值 $\\mathbb t=\\{t_1,t_2,\\dots,t_N\\}$ ，回归问题的目标是利用这组训练集，寻找一个合适的模型，来预测一个新的数据点 $\\hat x$ 对应的目标值 $\\hat t$ 。记模型的参数为 $w$ ，模型对应的函数为 $y$ ，模型的预测值可以相应表示为 $y(x,w)$ 。

为了衡量模型的好坏，需要一种方法衡量预测值与目标值之间的误差，一个常用的选择是平方误差和：

$E(w)=\\frac12\\sum_{n=1}^N\\{y(x_n,w)-t_n\\}^2$

平方误差和函数可以看成是每个数据点 $x_n$ 的预测值 $y(x_n,w)$ 到真实目标值 $t_n$ 的误差平方和的一半。

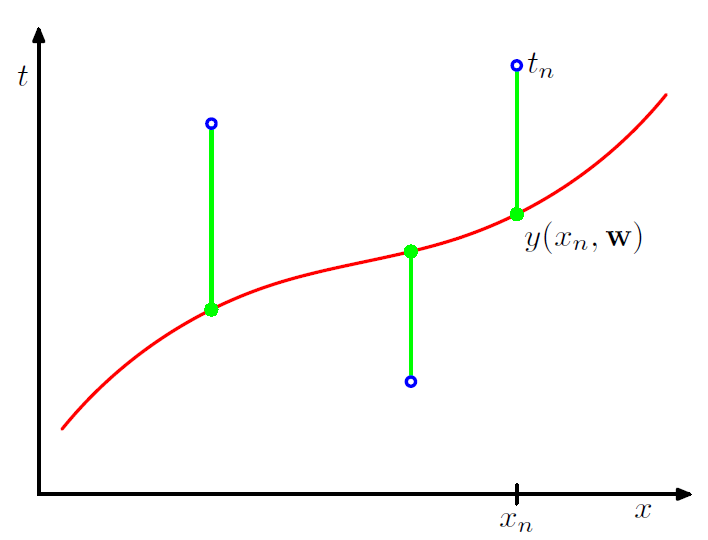
不同的参数 $w$ 对应于不同的误差函数 $E(w)$ ，因此，回归问题的目标通常是找到一组参数 $w^\\star$ 使得误差函数 $E(w)$ 最小化。

那么最小化 $E(w)$ 究竟有什么意义呢？

在回答这个问题之前，我们需要先复习一下概率知识。

先复习一下与条件概率相关的贝叶斯公式：

$p(x|y)=\\frac{p(y|x)p(x)}{p(y)}$

对于回归问题来说，如果我们记训练集为 $\\mathcal D$ ，那么对于模型参数 $w$ 来说，贝叶斯公式给出：

$p(w|\\mathcal D)=\\frac{p(\\mathcal D|w)p(w)}{p(\\mathcal D)}$

其中 $p(w)$ 表示的是参数 $w$ 的先验（prior）分布； $p(\\mathcal D|w)$ 给定参数为 $w$ 的情况下，训练数据为 $\\mathcal D$ 的可能性，我们也可以把它看成一个关于 $w$ 的函数，这个函数叫做似然函数（likelihood function）； $p(w|\\mathcal D)$ 是参数 $w$ 在给定数据 $\\mathcal D$ 下的后验（posterior）分布。

给定这些定义，贝叶斯公式可以表示成：

$\ ext{posterior}\\propto \ ext{likelihood}\ imes\ ext{prior}$

即后验正比于似然乘以先验。

似然函数是一个非常重要的概念。通过极大似然函数 $p(\\mathcal D|w)$ ，我们可以找到一个最优的参数 $w^\\star$ ，使得在这组参数设定下，出现训练数据 $\\mathcal D$ 的可能性 $p(\\mathcal D|w)$ 最大。这组参数在统计上叫做参数 $w$ 的极大似然估计。

早在上初中的时候，我们就学到了在做实验时，需要多次测量取平均来减少误差的道理。我们也知道，误差会来自两个部分：系统误差和随机误差。通过多次测量能够减少随机误差，但是不能减少系统误差，所以测量误差是不可避免的。

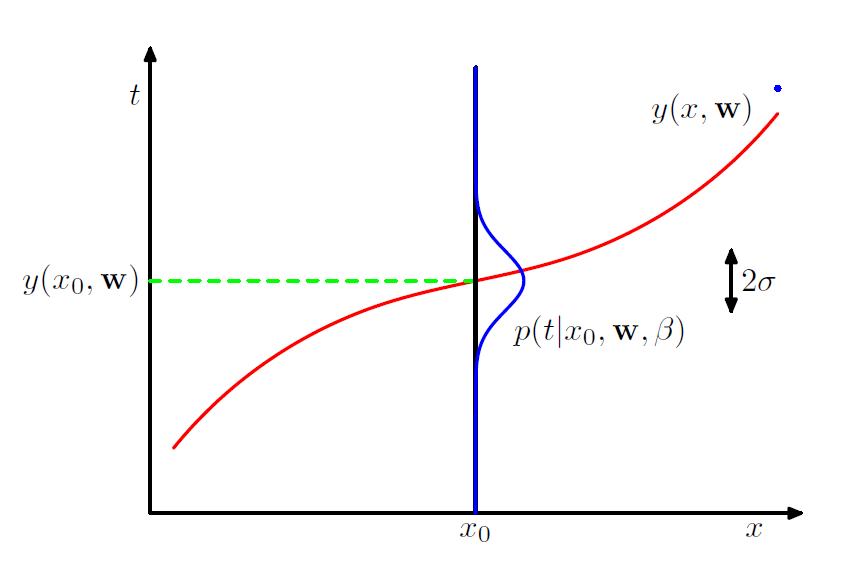
同样道理，在回归问题中， $x$ 的测量值 $t$ 会存在一定的误差。

假定对所有的数据点 $x$ ，模型预测值 $y(x,w)$ 与目标值 $t$ 之间的误差是一样的，并服从一定的概率分布，比如均值为0，方差为 $\\beta^{-1}=\\sigma^2$ 的高斯分布，则有：

$p(t-y(x,w)|x,w,\\beta) \\sim \\mathcal N(t-y(x,w)|0,\\beta^{-1})$

即：

$p(t|x,w,\\beta)\\sim\\mathcal N(t|y(x,t),\\beta^{-1})$

对于一组独立同分布的数据点 $\\mathbb x\\equiv\\{x_1,x_2,\\dots,x_N\\}$ ，以及这些数据对应的目标值 $\\mathbb t=\\{t_1,t_2,\\dots,t_N\\}$ ，我们得到关于这组数据的似然函数：

$p(\\mathsf t|\\mathsf x,w,\\beta^{-1})=\\prod_{n=1}^N p(t_n|x_n,w,\\beta^{-1})=\\prod_{n=1}^N \\mathcal N(t_n|y(x_n,w),\\beta^{-1})$

其中，高斯分布的概率函数为：

$N(t|y(x,t),\\beta^{-1})=\\left(\\frac{\\beta}{2\\pi}\\right)^{\\frac 12}\\exp \\left\\{-\\frac{\\beta}2\\left[t-y(x,w)\\right]^2\\right\\}$

可以通过极大化这个似然函数得到关于 $w$ 的一组极大似然解。

不过，更方便的做法是极大对数似然函数，因为对数函数是严格单增的，所以极大对数似然的解与极大似然的解是相同的。

对数似然函数为：

$\\ln p(\\mathsf t|\\mathsf x,w,\\beta^{-1})=-\\frac{\\beta}{2}\\sum_{n=1}^N\\{y(x_n,w)-t\\}^2+\\frac N 2\\ln \\beta-\\frac N 2\\ln 2\\pi$

如果我们不考虑 $\\beta$ 的影响，那么，对于参数 $w$ 来说，最小化平方误差和的解，就等于极大对数似然的估计。

因此，最小化平方误差和 $E(w)$ 与极大似然等价，考虑到似然函数的定义，优化 $E(w)$ 相当于在给定高斯误差的假设下，寻找一组 $w$ 使得观察到目标值t的概率最大。

现在考虑另一类问题——分类问题。

我们同样给出定义：

给定一个包含 $N$ 个数据样本的训练集 $\\mathbb x\\equiv\\{x_1,x_2,\\dots,x_N\\}$ ，以及这些数据对应的类别 $\\mathbb t=\\{t_1,t_2,\\dots,t_N\\}$ ，这里， $t_n\\in\\{1,2,\\dots,K\\}$ ，分类问题的目标是利用这组训练集，寻找一个合适的模型，来预测一个新的数据点 $\\hat x$ 对应的类别 $\\hat t$ 。现在假设模型的参数为 $w$ ，模型输出是属于每一类的概率，预测为第 $k\\in \\{1,2,\\dots,K\\}$ 类的概率为 $p(k|x,w)$ 。

对于样本 $x$ ，其属于第 $t$ 类的概率为：

$p(t|x,w)=\\prod_{k=1}^K p(y=t|x,w)^{1_{t=k}}$

其中， $1_{t=k}=\\left\\{\\begin{align}&1, & t=k\\\\ &0, & t\ eq k\\\\ \\end{align}\\right.$ 。

因此，似然函数为：

$p(\\mathsf t|\\mathsf x, w)=\\prod_{n=1}^N(\\prod_{k=1}^K p(t_n|x_n,w)^{1_{t=k}})$

对数似然为：

$\\ln p(t|x,w)=\\sum_{n=1}^N \\sum_{k=1}^K 1_{t=k}\\log p(t_n|x_n,w)$

极大化对数似然，相当于极小化：

$-\\sum_{n=1}^N \\sum_{k=1}^K 1_{t=k}\\log p(t_n|x_n,w)$

事实上，这正是我们常使用的多类交叉熵损失函数的表示形式。

因此，在分类问题中，最小化交叉熵损失函数相当与极大样本的似然函数。

在优化目标函数时，除了正常的损失函数外，为了防止过拟合，我们通常会加入一些正则项，比如权值衰减（weight decay），lasso等等。

比如，在回归问题中，使用权值衰减后，目标函数可能是：

$E(w)=\\frac 1 2\\sum_{n=1}^N\\{y(x_n,w)-t\\}^2 +\\lambda w^\ op w$

这里，我们假定 $w$ 可以被拉长表示为一个一维向量。

此时，优化这个目标函数就不能用极大似然来解释了。

不过，如果我们观察贝叶斯公式：

$p(w|\\mathcal D)=\\frac{p(\\mathcal D|w)p(w)}{p(\\mathcal D)}$

以及：

$\ ext{posterior}\\propto \ ext{likelihood}\ imes\ ext{prior}$

我们会发现，如果对两边取对数，那么有：

$\\ln p(w|\\mathcal D)=\\ln p(\\mathcal D|w)+ \\ln p(w) + const$

那么，我们加入的正则项，是不是对应于 $w$ 的先验分布 $p(w)$ 呢？

答案当然是肯定的。

如果给出参数 $w$ 的先验，那么极大后验估计（Maximize a Posterior, MAP）是能给出类似带正则项目标函数 $E(w)$ 的结构的。

问题是什么样的先验会给出类似权值衰减的正则项呢？

一个通常的想法是我们认为参数 $w$ 服从的先验分布是一个均值0，方差 $\\alpha^{-1}I$ 的D维高斯分布，那么，我们有：

$p(w|\\alpha)=\\mathcal N(0,\\alpha^{-1}I)=\\left(\\frac{\\alpha}{2\\pi}\\right)^{\\frac D 2}\\exp \\left\\{-\\frac \\alpha 2 w^\ op w \\right\\}$

其对数为：

$\\ln p(w|\\alpha)=-\\frac \\alpha2 w^\ op w + const$

结合我们之前的推导，我们有： $\\ln p(w|\\mathsf t, \\mathsf x,\\beta,\\alpha)=\\ln p(\\mathsf t|\\mathsf x,w,\\beta) + \\ln p(w|\\alpha)=-\\frac \\beta 2\\sum_{n=1}^N\\{y(x_n,w)-t\\}^2 -\\frac \\alpha 2 w^\ op w + const$

因此，加权值衰减的正则与高斯分布先验下极大后验估计的结果一致。

对于分类问题，该结论依然成立。

我们已经将解释了目标函数中，优化某些损失函数和正则项的意义。在解释更多的损失函数和正则项之前，需要先解决一个问题。

为什么是高斯分布？怎么老是高斯分布？

先给出结论：

对于一个连续随机变量 $x$ ，在给定均值和方差的约束下，交叉信息熵最大的分布是高斯分布。

熵是描述系统混乱度的概念，热力学第二定律告诉我们，在没有外力作用时，熵总是趋于自增的，因此，上面的结论告诉我们，生活中很多现象服从高斯分布并不是偶然。

先引出信息熵的概念。

先考虑一个离散随机变量 $X$ ，给定一个该随机变量的观察值 $x$ ，希望用一个函数 $h(x)$ 去衡量 $x$ 所携带的信息量。一般来说，如果 $x$ 是一件概率很低的事情，那么我们会觉得它很有信息量，反之，如果 $x$ 是一件经常发生的事情，那么我们会觉得信息量很少。因此，信息量会和 $x$ 发生的概率 $p(x)$ 相关。

另一方面，我们认为，如果两个事件 $x$ 和 $y$ 是相互独立的，那么，我们认为两者携带的信息量是各自信息量之和：

$h(x,y)=h(x)+h(y)$

另一方面。独立性给出：

$p(x,y)=p(x)p(y)$

再考虑约束，当 $p(x)=1$ 时， $h(x)=0$ ，不难看出，符合条件的是概率密度的对数函数，不妨定义为：

$h(x)=-\\log_2 p(x)$

这里，使用2为底的对数并不是必须的，也可以使用其他底。不过使用2为底，信息的单位就变成了bit。

对于一个离散分布 $X$ 来说，其信息的期望为：

$H[x]=-\\sum_x p(x)\\log_2 p(x)$

我们把 $H[x]$ 叫做这个随机变量的熵。

比如说，对于一个等概率，取值为8个的离散分布，其熵为：

$H=-8\ imes\\frac 1 8 \ imes \\log \\frac 1 8=3~bits$

3比特正是用2进制表示这8个值所需要的大小。

再比如说，考虑取值为 $a,b,c,d$ ，概率为： $\\frac 1 2, \\frac 1 4, \\frac 1 8, \\frac 1 8$ 的分布，其熵为：

$H=-\\frac 1 2\\log_2 \\frac12-\\frac 1 4\\log_2 \\frac14-2\ imes\\frac 1 8\\log_2 \\frac18=1.75~bits$

而这正是用霍夫曼编码a：0，b：10，c：110，d：111表示这四个值的平均比特大小。

除了以2为底，我们还可以以其他对数为底，比如自然对数：

$H[p]=-\\sum_xp(x)\\ln p(x)$

连续分布：

$H[p]=-\\int_x p(x)\\ln p(x) dx$

现在假设某个分布满足：

$\\int_x p(x)dx=1$

$\\int_x xp(x)dx=\\mu$

$\\int_x (x-\\mu)^2p(x)dx=\\sigma^2$

在这些假设下，为了使 $H[p]$ 最大，其Lagrange函数为：

$-\\int_x p(x)\\ln p(x) dx +\\lambda_1(\\int_x p(x)ds-1) +\\lambda_2(\\int_xxp(x)dx-\\mu) +\\lambda_3(\\int_x (x-\\mu)^2p(x)dx-\\sigma^2)$

即：

$\\int_x[-p\\ln p+\\lambda_1 p+\\lambda_2xp+\\lambda_3(x-\\mu^2)p]~dx + const=\\int_x G(p, x)dx + const$

利用变分法中的欧拉-拉格朗日方程

$\\frac{\\partial G}{\\partial p}-\\frac{d}{dx}\\left(\\frac{\\partial G}{\\partial p'}\\right)=0$

我们得到使得 $H[p]$ 最大的 $p(x)$ 需要满足：

$\\ln p(x)=-1+\\lambda_1+\\lambda_2x+\\lambda_3(x-\\mu)^2$

即：

$p(x)=\\exp (-1+\\lambda_1+\\lambda_2x+\\lambda_3(x-\\mu)^2)$

带入约束中，不难解出：

$p(x)=\\frac 1{\\sqrt{2\\pi}\\sigma}\\exp \\left\\{\\frac{(x-\\mu)^2}{2\\sigma^2}\\right\\}$

即高斯分布是满足约束下，熵最大的分布。

接下来，我们讨论其他的损失函数与正则。

事实上，如果我们考虑更一般的分布：

$p(x|\\sigma^2,q)=\\frac{q}{2(2\\sigma^2)^{1/q}\\Gamma(1/q)}\\exp\\left\\{-\\frac{|x|^q}{2\\sigma^2}\\right\\}$

不难得出：

$\\ln p(x|\\sigma^2,q)=-\\frac{|x|^q}{2\\sigma^2}+const$

在回归问题中，如果我们用这个分布作为预测值与目标值之间误差的分布：

$t=y(x,w)+\\epsilon, ~\\epsilon\\sim p(\\epsilon|\\sigma^2,q)$

那么，对应的损失函数为 $L_q$ 损失函数：

$|y(x,w)-t|^q$

如果我们认为参数 $w$ 的先验服从该分布：

$w\\sim p(w|\\sigma^2,p)$

那么，对应的正则项为 $L_p$ 正则项：

$|w|_p$

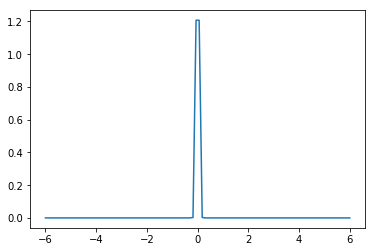
当 $p=1$ 时，我们相当于加了一个 $L_1$ 范数的正则项，即Lasso，它通常具有稀疏的作用，原因是此时参数的先验分布大概长这个样子：

总而言之，优化损失函数与正则项，其实代表的是对参数 $w$ 的极大似然或者极大后验估计，不同的损失函数和正则项，反映的我们对参数先验分布和似然函数的不同假设。

[1]Christopher, M. Bishop. "Pattern recognition and machine learning." Company New York 16.4 (2006): 049901.

上一篇：9是什么意思网络用语

下一篇：线下餐饮行业线上营销方法有哪些？

[返回列表]